Apr 10, 2018 · post

PyTorch for Recommenders 101

Recommenders, generally associated with e-commerce, sift though a huge inventory of available items to find and recommend ones that a user will like. Different from search, recommenders rely on historical data to tease out user preference. How does a recommender accomplish this? In this post we explore building simple recommendation systems in PyTorch using the Movielens 100K data, which has 100,000 ratings (1-5) that 943 users provided on 1682 movies.

Matrix Factorization

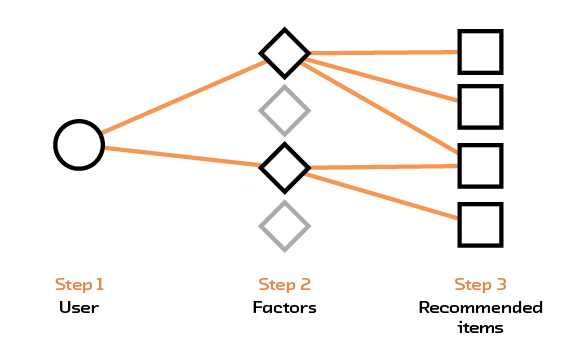
We first build a traditional recommendation system based on matrix factorization. The input data is an interaction matrix where each row represents a user and each column represents an item. The rating assigned by a user for a particular item is found in the corresponding row and column of the interaction matrix. This matrix is generally large but sparse; there are many items and users but a single user would only have interacted with a small subset of items. Matrix factorization decomposes this larger matrix into two smaller matrices - the first one maps users into a set of factors and the second maps items into the same set of factors. Multiplying these two smaller matrices together gives an approximation to the original matrix, with values for empty elements inferred. To predict a rating for a user-item pair, we simply multiply the row representing the user from the first matrix with the column representing the item from the second matrix.

In PyTorch we can implement a version of matrix factorization by using the embedding layer to “map” users into a set of factors. The number of factors determine the size of the embedding vector. Similarly we map items into their own embedding layer. Both user and item embeddings have the same size. To predict a user-item rating, we multiply the user embeddings with item embeddings and sum to obtain one number. The following code draws from Ethan Rosenthal’s work on matrix factorization in PyTorch.

import torch
from torch.autograd import Variable

class MatrixFactorization(torch.nn.Module):
    def __init__(self, n_users, n_items, n_factors=20):
        super().__init__()
	# create user embeddings
        self.user_factors = torch.nn.Embedding(n_users, n_factors,
                                               sparse=True)
	# create item embeddings
        self.item_factors = torch.nn.Embedding(n_items, n_factors,
                                               sparse=True)

    def forward(self, user, item):
    	# matrix multiplication
        return (self.user_factors(user)*self.item_factors(item)).sum(1)

    def predict(self, user, item):
        return self.forward(user, item)

To fit the matrix factorization model we need to pick a loss function and an optimizer. In this example we use the average squared distance between the prediction and the actual value as a loss function, this is known as mean-squared error. We then try to minimize this loss by using stochastic gradient descent. The code below shows how the model is fitted in four steps: i) pass in a user-item pair, ii) forward pass to compute the predicted rating, iii) compute the loss, and iv) backpropagate to compute gradients and update the weights.

model = MatrixFactorization(n_users, n_items, n_factors=20)
loss_fn = torch.nn.MSELoss() 
optimizer = torch.optim.SGD(model.parameters(),
                            lr=1e-6)

for user, item in zip(users, items):
    # get user, item and rating data
    rating = Variable(torch.FloatTensor([ratings[user, item]]))
    user = Variable(torch.LongTensor([int(user)]))
    item = Variable(torch.LongTensor([int(item)]))

    # predict
    prediction = model(user, item)
    loss = loss_fn(prediction, rating)

    # backpropagate
    loss.backward()

    # update weights
    optimizer.step()

We train this model on the Movielens dataset with ratings scaled between [0, 1] to help with convergence. Applied on the test set, we obtain a root mean-squared error(RMSE) of 0.66. This means that on average, the difference between our prediction and the actual value is 0.66!

Dense Feedforward Neural Network

Given the underwhelming performance of our matrix factorization model, we try a simple feedforward recommendation system instead. The input to this neural network is a pair of user and item represented by their IDs. Both user and item IDs first pass through an embedding layer. The output of the embedding layer, which are two embedding vectors, are then concatenated into one and passed into a linear network. The output of the linear network is one dimensional - representing the rating for the user-item pair. The model is fit the same way as the matrix factorization model and uses the standard PyTorch approach of forward passing, computing the loss, backpropagating and updating weights.

import torch
import torch.nn.functional as F
from torch.autograd import Variable
from torch import nn

class DenseNet(nn.Module):

    def __init__(self, n_users, n_items, n_factors, H1, D_out):
        """
        Simple Feedforward with Embeddings
        """
        super().__init__()
   	# user and item embedding layers
        self.user_factors = torch.nn.Embedding(n_users, n_factors,
                                               sparse=True)
        self.item_factors = torch.nn.Embedding(n_items, n_factors,
                                               sparse=True)
   	# linear layers
        self.linear1 = torch.nn.Linear(n_factors*2, H1)
        self.linear2 = torch.nn.Linear(H1, D_out)

    def forward(self, users, items):
        users_embedding = self.user_factors(users)
        items_embedding = self.item_factors(items)
	# concatenate user and item embeddings to form input
        x = torch.cat([users_embedding, items_embedding], 1)
        h1_relu = F.relu(self.linear1(x))
        output_scores = self.linear2(h1_relu)
        return output_scores

    def predict(self, users, items):
        # return the score
        output_scores = self.forward(users, items)
        return output_scores

Once again, we train this model on the Movielens dataset with ratings scaled between [0, 1] to help with convergence. Applied on the test set, we obtain a root mean-squared error(RMSE) of 0.28, a substantial improvement!

Sequence based Recommendation System

Finally we build a recommendation system that takes into account the sequence of item interactions. The heart of this is a Long Short-Term Memory (LSTM) cell, a variant of Recurrent Neural Networks (RNN) with faster convergence and better long term memory. The input to this system is a history of item interactions and their corresponding ratings. In the following example of an input, we show a sequence of item interaction of length 10 (arbitrarily chosen) and the corresponding rating. Elements in the first array correspond to items(movies), and elements in the second array correspond to ratings. We see that, for example, movie 209 has a rating of 4, and movie 32 has a rating of 5. Sequences shorter than 10 are padded with zeros.

In [2]: training_data[0]
Out[2]: 
(array([209,  32, 189, 242, 171, 111, 256,   5,  74, 102], dtype=int32),
 array([4, 5, 3, 5, 5, 5, 4, 3, 1, 2], dtype=int32))

Items are passed through an embedding layer before going into the LSTM. The output of the LSTM is then fed into a linear layer with an output dimension of one. The LSTM has 2 hidden states, one for short term memory and one for long term. Both states need to be initialized.

PyTorch expects LSTM inputs to be a three dimensional tensor. The first dimension is the length of the sequence itself, the second represents the number of instances in a mini-batch, the third is the size of the actual input into the LSTM. Using our training data example with sequence of length 10 and embedding dimension of 20, input to the LSTM is a tensor of size 10x1x20 when we do not use mini batches. For a mini-batch size of 2, each forward pass will have two sequences, and the input to the LSTM needs to have a dimension of 10x2x20. LSTMs take variable input sequence lengths but for batch training purposes the input data is generally processed(with padding if necessary) to have a fixed length.

import torch
import torch.nn as nn
from torch.autograd import Variable

class LSTMRating(nn.Module):

    def __init__(self, embedding_dim, hidden_dim, num_items, num_output):
        super().__init__()
        self.hidden_dim = hidden_dim
        self.item_embeddings = nn.Embedding(num_items, embedding_dim)
        self.lstm = nn.LSTM(embedding_dim, hidden_dim)
        self.linear = nn.Linear(hidden_dim, num_output)
        self.hidden = self.init_hidden()

    def init_hidden(self):
    	# initialize both hidden layers
        return (Variable(torch.zeros(1, 1, self.hidden_dim)),
                Variable(torch.zeros(1, 1, self.hidden_dim)))

    def forward(self, sequence):
        embeddings = self.item_embeddings(sequence)
        output, self.hidden = self.lstm(embeddings.view(len(sequence), 1, -1),
                                        self.hidden)
        rating_scores = self.linear(output.view(len(sequence), -1))
        return rating_scores

    def predict(self, sequence):
        rating_scores = self.forward(sequence)
        return rating_scores

Once the neural network is defined, we fit the training data using stochastic gradient descent with a mean squared error loss function.

embedding_dim = 64
hidden_dim = 128
n_output = 1

# add one to represent padding when there is not enough history
model = LSTMRating(embedding_dim, hidden_dim, n_items+1, n_output)
loss_fn = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.1)

for sequence, target_ratings in training_data:
    model.zero_grad()
    # initialize hidden layers
    model.hidden = model.init_hidden()
    # convert sequence to PyTorch variables
    sequence_var = Variable(torch.LongTensor(sequence.astype('int64')))
    # forward pass
    ratings_scores = model(sequence_var)
    target_ratings_var = Variable(torch.FloatTensor(target_ratings.astype('float32')))
    # compute loss
    loss = loss_fn(ratings_scores, target_ratings_var)
    # backpropagate
    loss.backward()
    # update weights
    optimizer.step()

Similar to other models, we train the LSTM-based model on the Movielens dataset with ratings scaled between [0, 1] to help with convergence. Applied on the test set, we obtain a root mean-squared error(RMSE) of 0.43 - the LSTM model underperforms the dense feed forward network.

Post-amble

The models discussed in this post are basic building blocks for a recommendation system in PyTorch. There are no bells and whistles and we did not attempt to fine tune any hyperparameters. Our first pass result suggests that the dense network performs best, followed by the LSTM network and finally the matrix factorization model. The root mean-squared error (RMSE) are 0.28, 0.43 and 0.66 respectively on the Movielens 100K dataset with ratings scaled between [0, 1]. We thought PyTorch was fun to use; models can be built and swapped out relatively easily. When we did encounter errors, most of them were triggered by incorrect data types.

For more on recommendations, please see our Semantic Recommendations report, where we focus on how machines can better understand content!