Apr 3, 2019 · post
An Invitation to Active Learning
Many interesting learning problems exist in places where labeled data is limited. As such, much thought has been spent on how best to learn from limited labeled data. One obvious answer is simply to collect more data. That is valid, but for some applications, data is difficult or expensive to collect. If we will collect more data, we ought at least be smart about the data we collect. This motivates active learning, which provides strategies for learning in this scenario.
The ideal setting for active learning is that in which we have a small amount of labeled data with which to build a model and access to a large pool of unlabeled data. We must also have the means to label some of that data, but it’s OK for the labeling process to be costly (for instance, a human hand-labeling an image). The active learning process forms a loop:
- build a model based on the labeled data available
- use the model to predict labels for the unlabeled points
- use an active learning strategy to decide which point to label next
- label that point
- GOTO 1.
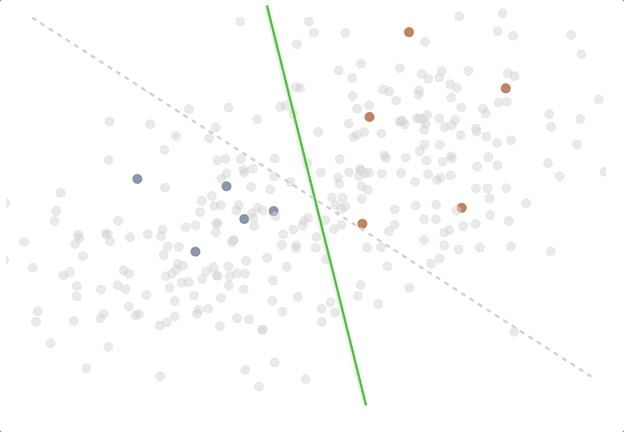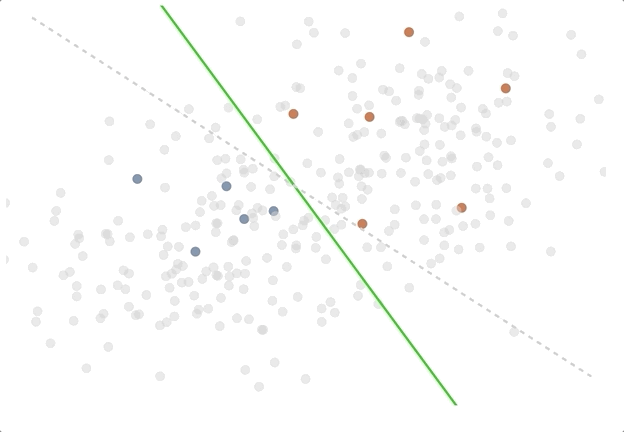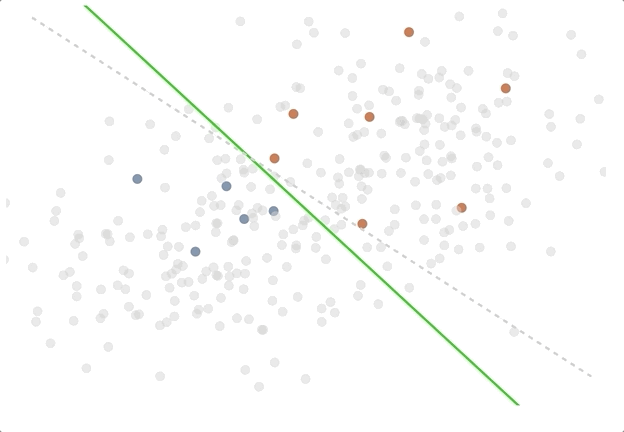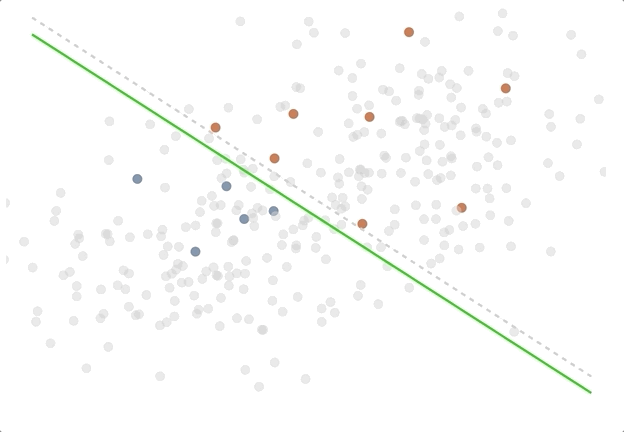The active learning loop in action - try out the demo!
The essence of active learning is in the strategy we choose in the loop above. Three broad families of strategy are:
-
Random sampling. In the default case, we sample unlabeled data from the pool randomly. This is a passive approach where we don’t use the output of the current model to inform the next data point to be labeled. As such, it isn’t really active learning.
-
Uncertainty sampling. In uncertainty sampling, we choose the data point about which the algorithm is least certain to label next. This could be the point closest to the decision boundary (the least confident prediction), or it could be the point with highest entropy, or other measure of uncertainty. Choosing points as such helps our learning algorithm refine the decision boundary.
-
Density sampling. Uncertainty sampling works much better than random sampling, but by definition it causes the data points we choose to label to cluster around the decision boundary. This data may be very informative, but not necessarily representative. In density sampling, we try to sample from regions where there are many data points. The trade off between informativeness and representativeness is fundamental to active learning, and there are many approaches that address it.
To illustrate the difference between passive and active learning, we created an Observable notebook with a toy problem, which you can explore here. In the notebook, the goal is to find a good separation of red and blue points on a two dimensional chart, and we train a logistic regression model live in the browser to do so. One can see how the decision boundary separating the points evolves as more data is labeled with a random sampling strategy, and also with an uncertainty sampling strategy. In the case of two classes with a linear decision boundary, all the uncertainty sampling strategies (least confidence and highest entropy) give the same result. This is an extremely simplified example, but we think it shows some of the intuition behind active learning.
We explore active learning in much more detail in our report Learning with Limited Labeled Data, and you can get a high level overview in our previous post.
