Jul 31, 2018 · newsletter

New Dynamics for Topic Models

Topic models can extract key themes from large collections of documents in an unsupervised manner, which makes them one of the most powerful tools in organizing, searching, and understanding the vast troves of text data produced by humanity. Their power derives, in part, from their in-built assumptions about the nature of text; specifically, to identify topics, the model has to give the notion of a topic a mathematical structure that echoes its significance to a human reader. In their recent paper, Scalable Generalized Dynamic Topic Models, Patrick Jähnichen, Florian Wenzel, Marius Kloft, and Stephan Mandt show scalable models that allow topics to change over time in a way that is more general than it was previously, extracting new forms of patterns from large-scale datasets.

Probabilistic Topic Models: from Static to Dynamic

Jähnchen et al.‘s work builds on the shift towards probabilistic topic models that was cemented by the publication of David Blei, Andrew Ng, and Michael Jordan’s seminal Latent Dirichlet Allocation (LDA) in 2003. The context, at the time, was given in particular by Latent Semantic Indexing (LSI) (1990), which relies on finding linear combinations of tf-idf features that explain the greatest amount of variation in a corpus. Topics, in that case, are then weighted collections of words that are particularly discriminative with respect to identifying individual documents in the corpus, and finding them requires the singular value decomposition of a document matrix.

In contrast, probabilistic topic models rely on reverse engineering an imagined statistical process that generates the documents, in which the topics are latent parameters that are inferred from the raw corpus data. The generative process for LDA, for example, is a hierarchical Bayesian model that assumes that each word within a document is drawn from one of several multinomial distributions that correspond to topics. The mixture of topics in each document, i.e. the probability with which one of the multinomial distributions will give rise to a word in the document, is in turn determined by drawing from a Dirichlet distribution. Writing this out results in an intractable expression for the probability of each word, which is conditional on the topic parameters and can be fitted to the corpus using a host of well-known methods (as well as, conveniently, packages like gensim and sklearn).

Of course, the inference process is considerably more difficult than the linear algebra required of LSI, but the process of designing a generative process makes it possible to imbue the topics with properties that highlight aspects of interest, or that make the topic model more realistic. For example, one might allow for topics to be correlated in the way that they co-occur within a document. At the expense of having to fit additional parameters, this enables surfacing topic relationships.

With Dynamic Topic Models (2006), David Blei and John Lafferty revisited the LDA process to tackle the problem of topics changing over time. While the original LDA model ignores any ordering of the documents in the corpus, dynamic topic models will take their time stamps into account. Blei and Lafferty did so by allowing the topic parameters to wander over time, specifically by imposing upon them a Wiener Process, also known as Brownian Motion. The results are highly compelling: in their paper, they analyze over a century of Science magazine articles, and automatically extract a small history of neuroscience and atomic physics. (Blei happens to be an excellent lecturer, and those looking for his talks online will find a more comfortable introduction to ideas in topic modeling than is provided by the technical papers.)

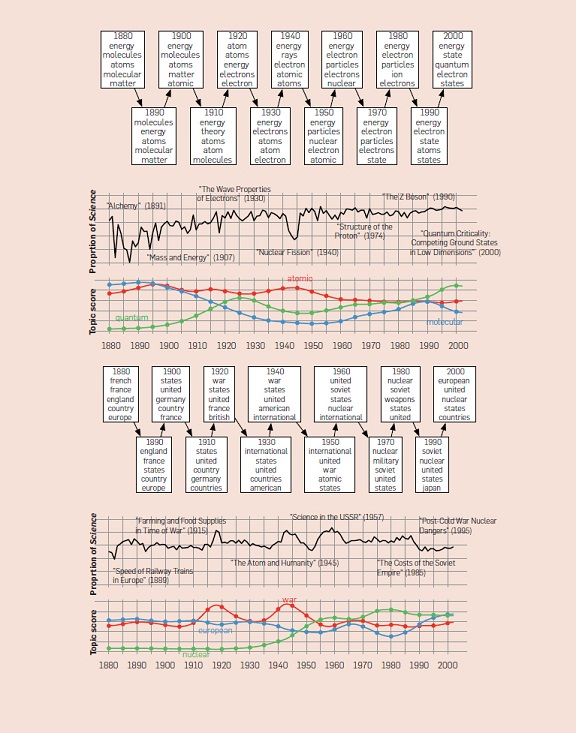
Time Evolution of two topics within the Science corpus. From: D. Blei, Probabilistic Topic Models, Communications of the ACM (2012)

Scalable New Dynamics

A Wiener process is convenient in several ways. It describes a random walk in which the value after each time step is simply the last time step, plus a random increment that is drawn from a normal distribution. In case of the LDA topic model, this allows for the multinomial distributions that represent the topics to undergo an incremental drift. In this way, the topics can change, albeit slowly enough to draw statistical robustness from older document data. The simplicity of the Wiener process also introduces temporal dynamics with the minimum number of additional parameters, and, given the difficulty of performing scalable approximate inference on topic models that implement dynamical stochastic process priors, had so far been the only process for which inference was feasible.

Jähnchen and colleagues now managed to substantially extend the spectrum of time dynamics to the general class of Gaussian Processes, of which the Wiener process is the simplest subcase. Gaussian processes are completely defined by their mean and covariance function in the same way in which a Gaussian distribution is completely defined by mean and variance, and just like the Gaussian distribution, they simultaneously represent the simplest interesting case and are extremely broadly applicable. In the study, the authors proceed by exploring the new wealth of possible functions by implementing dynamic topic models based on a three common processes used in time series modeling, comparing each to the result based on the Wiener process. The processes, which represent a small subset of realizable properties, include:

1. Ornstein-Uhlenbeck:

Brownian motion in the presence of a mean reverting force (in physics, this would for example occur for a spring that is undergoing thermal noise).

2. Squared Exponential kernel:

A process with a memory over several previous time steps, in which the correlation with past time steps decreases exponentially. That is, the process has a short-term memory that can be tuned by changing the decay length.

3. Cauchy kernel:

A process that has memory, similar to the one that corresponds to the squared exponential kernel, but in this case, the correlation with past time steps decreases polynomially. The process has a long-term memory.

Based on large scale datasets, the authors reveal that each of these approaches reveals qualitatively different phenomena, and conclude that they offer better performance along the lines of interpretability and usefulness, as well as perplexity measures. However, the greatest strength is likely the ability to flexibly experiment with different types of processes toward different tasks: processes with short-term memory can be used for event detection, whereas long-term memory has greater statistical strength. The mean-reversion property acts as a type of regularization that responds to small-scale changes and localized topics in time. Adding and multiplying kernels also results in valid kernels, enabling considerable fine tuning. While deferred to future work, periodic kernels should be able to detect recurring events.

On the whole, playing with different processes enables practitioners to intuitively adapt and experiment with dynamic topic models to analyze time-stamped corpora in a targeted way, benefiting from the extensive experience that has been gathered by studying time series in general. Apart from growing in sophistication, topic models will also grow in diversity: as the authors indicated toward the conclusion of the paper, the selection of a prior is a modeling choice that helps reveal the effects that one searches for.